The book Geometric Transforms for Fast Geometric Algorithms introduces an interesting algorithm from page 84 of computing the diameter of a set of points in two dimensions. Inspired by this, I come up with a solution to computing the width of a set using geometric transformation.

Definition of the Width of a Set

Let $S$ be a set of $n$ points in $\mathbb{R}^2$. If $l$ and $l^\prime$ are two parallel lines, then the region between them is called a slab. The width of $S$ is defined to be the minimum distance between the bounding lines of any slab that contains all points of $S$.

Characterization of the Width

Before presenting the width-finding algorithm, I’d like first to characterize the width of a set of points, introduce some terminology, and prove several theorems.

When we say that $A$ is contained in $B$, it means that every point of $A$ also lies in $B$. The bounding lines of a slab could contain a vertex or an edge of the convex hull $H(S)$ of the set of points $S$.

Theorem 1: Let $l$ and $l^\prime$ be two parallel lines that define the width of $S$, both $l$ and $l^\prime$ contain a vertex of the convex hull $H(S)$ of $S$.

Proof. Assume otherwise. The width is determined by parallel lines $l$ and $l^\prime$, and $l$ contains a vertex of $H(S)$, $l^\prime$ does not, as shown in Figure 1. Then there must exist a line $l^{\prime\prime}$ closer to the set of points $S$ and produces a smaller distance. Q.E.D.

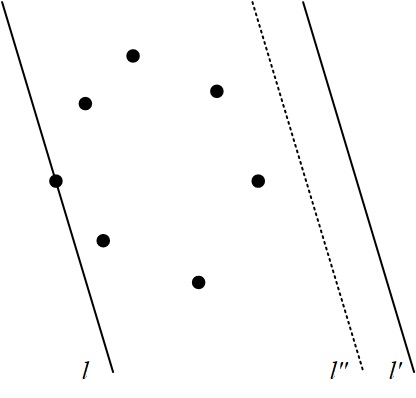
Theorem 2: Let $l$ and $l^\prime$ be two parallel lines that define the width of $S$, at least one of $l$ and $l^\prime$ contain an edge of the convex hull $H(S)$ of $S$.

Proof. Assume otherwise. The width is determined by parallel lines $l$ and $l^\prime$ which both pass a vertex but neither of them passes an edge. We can rotate the parallel lines in preferred direction of rotation which means we rotate $l$ and $l^\prime$ about the two vertices they pass to form new parallel lines $l_1$ and ${l_1}^\prime$, and the distance between $l_1$ and ${l_1}^\prime$ is smaller. This contradicts the assumption. Q.E.D.

Computing the Width

We can divide the convex hull into 2 parts: the upper hull and the lower hull, so that when one of the parallel lines of support of $S$ meets the convex hull on the upper hull, the other is on the lower hull.

According to the duality transformation, a non-vertical line $y=kx+b$ can be transformed into the point $(k,b)$ which is formed by the slope and intercept of the line. And a point $(a,b)$ can be transformed into the line $y=k(x-a)+b$ which means the set of lines that pass through it.

Hence, we define the transform of an edge of the convex hull $H(S)$ of $S$ as the slope of the line containing that edge and the transform of a vertex of $H(S)$ as the set of slopes of lines that pass through it. I.e., the line containing an edge $y=kx+b$ can be mapped to the one dimensional point $(k)$ and the vertex that lies between two edges $y=k_1x+b_1$ and $y=k_2x+b_2$ can be mapped to the closed interval $[k_1,k_2]$. As shown in Figure 2, the convex hull is transformed into a line that consists of an upper part and a lower part.

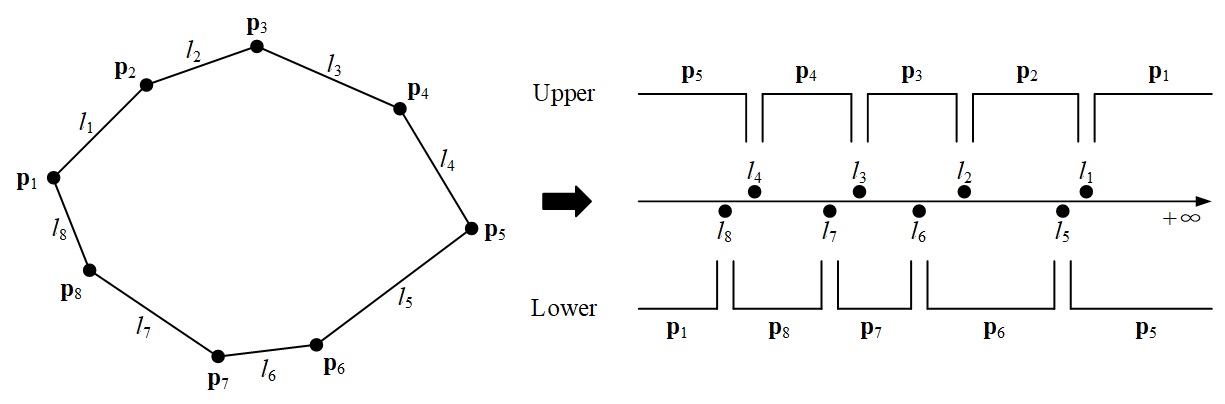
As the slopes of the edges of the convex hull are already sorted, when we transform the convex hull to a line, the upper and lower sets of points and intervals on the line are in sorted order.

As known from Theorem 1, the parallel lines of support pass through an edge and a vertex of the convex hull $H(S)$, which means the corresponding point and interval pair contained in the parallel lines must intersect on the upper and lower lines, e.g., $\mathbf{p}_5$ and $l_8$, $\mathbf{p}_6$ and $l_2$ in Figure 2.

Thus, finding the width of a set of points $S$ can be reduced to scanning the intersections of point and interval pairs on the upper and lower hulls of its convex hull $H(S)$.

To summarize, the width of a set of points $S$ can be computed in the following manner.

Begin

Step 1: Construct the convex hull $H(S)$ of $S$.

Step 2: Apply the transform to obtain two ordered sets of points and intervals.

Step 3: Scan the sets for intersections between the intervals of one set and the points of the other, generating the corresponding vertex and edge pair. For each such pair, compute the distance between the vertex and the extended edge, and note the smallest such distance. When the scan is complete, that distance is the width.

End

Time Complexity

According to the gift wrapping algorithm and the Graham scan algorithm, the running time of finding the convex hull of a set of points can be minimized to $O(n\log h)$, where $h$ is the number of points on the convex hull. And obtaining the two ordered sets and scanning the sets both takes $O(h)$ time. Therefore, finding the width of a set of points $S$ in $\mathbb{R}^2$ takes $O(n\log h)$ time.