Plane detection is a widely used technique that can be applied in many applications, e.g., augmented reality (AR), where we have to detect a plane to generate AR models, and 3D scene reconstruction, especially for man-made scenes, which consist of many planar objects. Nowadays, with the proliferation of acquisitive devices, deriving a massive point cloud is not a difficult task, which shows promise in doing plane detection in 3D point clouds.

Related Work

There are some existing plane detection and point cloud deep learning approaches proposed by recent researches.

Plane Detection in 3D Data

The 3D Hough transform is one possible approach for doing plane detection. As well as line detection in 2D space, planes can be parameterized into a 3D Hough space. The RAPter is another method that can be used for plane detection. It finds out the planes in a scene according to the predefined inter-plane relations, so RAPter is efficient for man-made scenes with significant inter-plane relations, but not adequate for some more general cases.

Deep Learning for 3D Data and Point Cloud

People have designed many deep learning approaches for different representations of 3D data. For instance, the volumetric CNN consumes volumetric data as input, and apply 3D convolutional neural networks to voxelized shapes. The multiview CNN projects the 3D shape into 2D images, and then apply 2D convolutional neural networks to classify them. The feature-based DNN focuses on generating a shape vector of the object according to its traditional shape features, and then use a fully connected net to classify the shape. The PointNet proposed a new design of neural network based on symmetric functions that can take unordered input of point clouds.

Design of Neural Networks

PointNet uses symmetric functions that can effectively capture the global features of a point cloud. Inspired by this, this experiment uses a symmetric network that concatenates global features and local features. Besides, for comparison, I also used a traditional network that simply generates a high dimensional local feature space by multilayer perceptions.

Symmetric Network

According to the universal approximation of symmetric function proposed by PointNet, a symmetric function $f$ can be arbitrarily approximated by a composition of a set of single-variable functions and a max pooling function, as described in Theorem 1.

Theorem 1: Suppose $f\colon\chi\to\mathbb{R}$ is a continuous set function w.r.t. Hausdorff distance $d_H$. $\forall\epsilon>0$, $\exists$ a continuous function $h$ and a symmetric function $g(\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n)=\gamma\circ\max$, such that for any $S\in\chi$,$$\begin{equation}|f(S)-\gamma(\max_{\mathbf{x}_i\in S}\{h(\mathbf{x}_i)\})|<\epsilon,\tag{1}\label{eq:1}\end{equation}$$where $\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n$ is the full list of elements in $S$ ordered arbitrarily, $\gamma$ is a continuous function, and $\max$ is a vector max operator that takes $n$ vectors as input and returns a new vector of the element-wise maximum.

Thus, according to Theorem 1, the symmetric network can be designed as a multi-layer perceptron network connected with a max pooling function, which is shown in Figure 1.

In order to achieve the invariance towards geometric transformation, an input alignment ($\mathbf{T}_1$ in Figure 1) and a feature alignment ($\mathbf{T}_2$ in Figure 1) are respectively applied to the input space and feature space. The points are first mapped to a 64-dimensional feature space and then mapped to a 1024-dimensional feature space. A max pooling function is applied to the 1024-dimensional feature space to generate a 1024-length global feature vector. The global vector is then concatenated to the 64-dimensional feature space which generates a 1088-dimensional space. Lastly, a 2-dimensional vector for each point, which represents the score for the planar part and non-planar part, is updated from the 1088-dimensional space.

Asymmetric Network

For doing a comparison, a traditional asymmetric network is also introduced in this experiment. It is basically modified from the symmetric network by detaching the max pooling function from the multi-layer perceptron network. The architecture of the asymmetric network is shown in Figure 2.

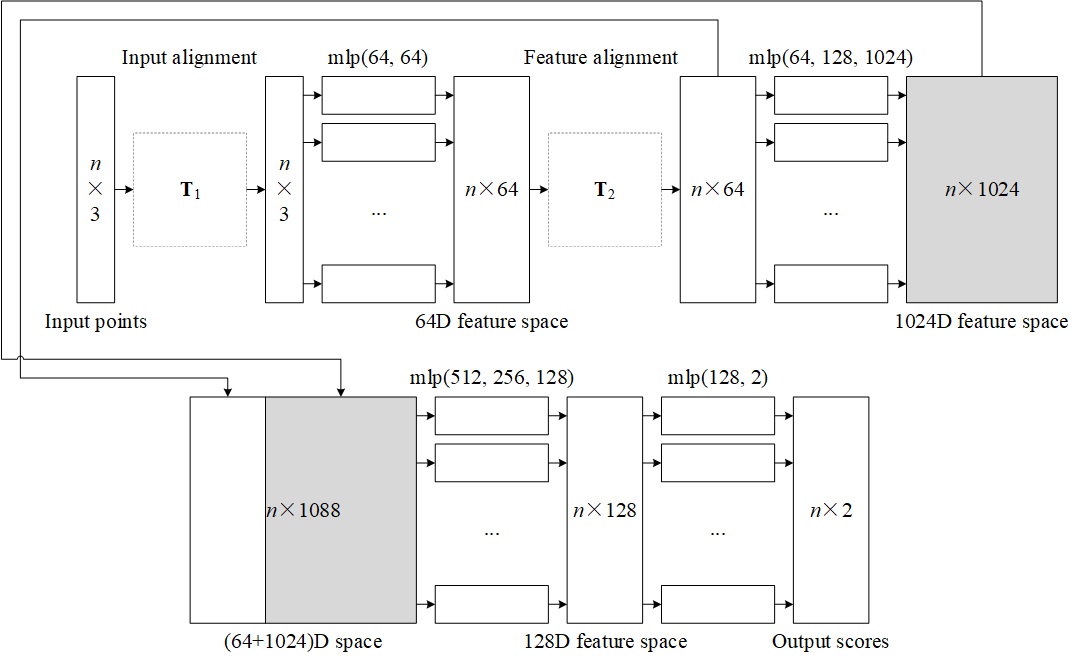
Instead of concatenating the global feature vector to the 64-dimensional feature space, the asymmetric network simply concatenates the 64-dimensional feature space and the 1024-dimensional feature space, and generates the 2-dimensional scores from that.

Experiment

The experiment is conducted in the following pattern: first, prepare the data for training and testing; then feed the training data respectively to the symmetric network and asymmetric network, and find the best-trained model according to the minimum total loss; lastly, compare the plane detection results of symmetric network and asymmetric network.

Experimental Data and Data Preprocessing

This experiment uses data from the ShapeNetPart dataset. I chose 64 tables, which have a significant planar surface, from the table repository for training, and 8 for testing and evaluation.

Each the point cloud was previously undersampled to a size of 2048 points, using a random sample. The point clouds for training were written into an HDF5 file, which contains 2 views, points and pid, respectively recording the point coordinate and the planar information associated with each point.

The planar parts were marked out manually on the original data. Figure 3 shows a few examples of table objects for training.

Best Trained Models

Basically, a point cloud contains more points in the non-planar part than points in the planar part. In order to handle this unbalanced data, I used a weighted cross-entropy function to calculate the mean loss for each epoch. The planar part is assigned with a weight of 0.7 and the non-planar part is assigned with a weight of 0.3.

Both networks are trained for 150 epochs. The plot of mean loss for training the symmetric network is shown in Figure 4.

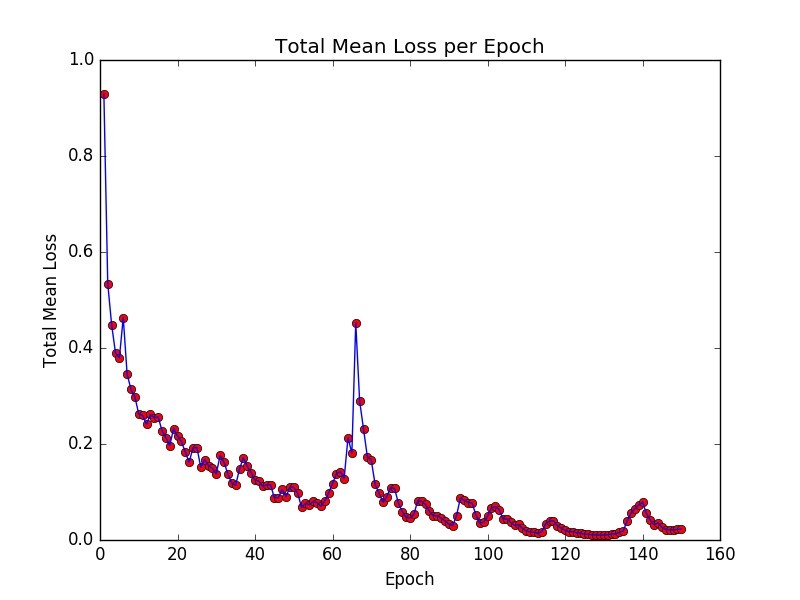
According to Figure 4, the total mean loss is stuck at a very low value after the 100th epoch, so I chose the trained model from the 130th epoch for testing.

Besides, Figure 5 is the plot of mean loss for training the asymmetric network.

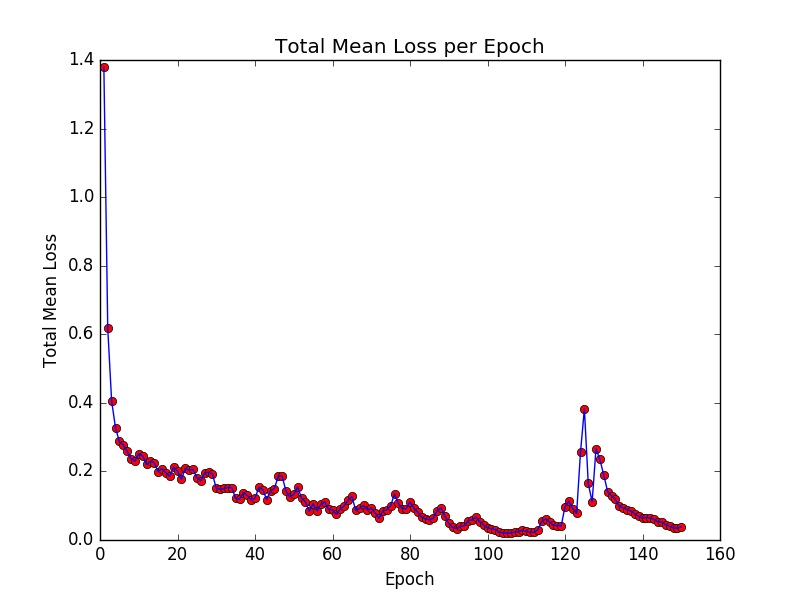
The loss value stays low after the 100th epoch, and there is a fluctuation around the 130th epoch. Such fluctuation may be caused by overfitting, so I chose the trained model from the 110th epoch for testing.

Experiment Results

The test set has a size of 8 objects. The test result for the model of the symmetric network shows an accuracy of 83.4534% and an Intersection over Union (IoU) of 71.1421%. Figure 6 illustrates the plane detection result in the test set using the model generated by the symmetric network.

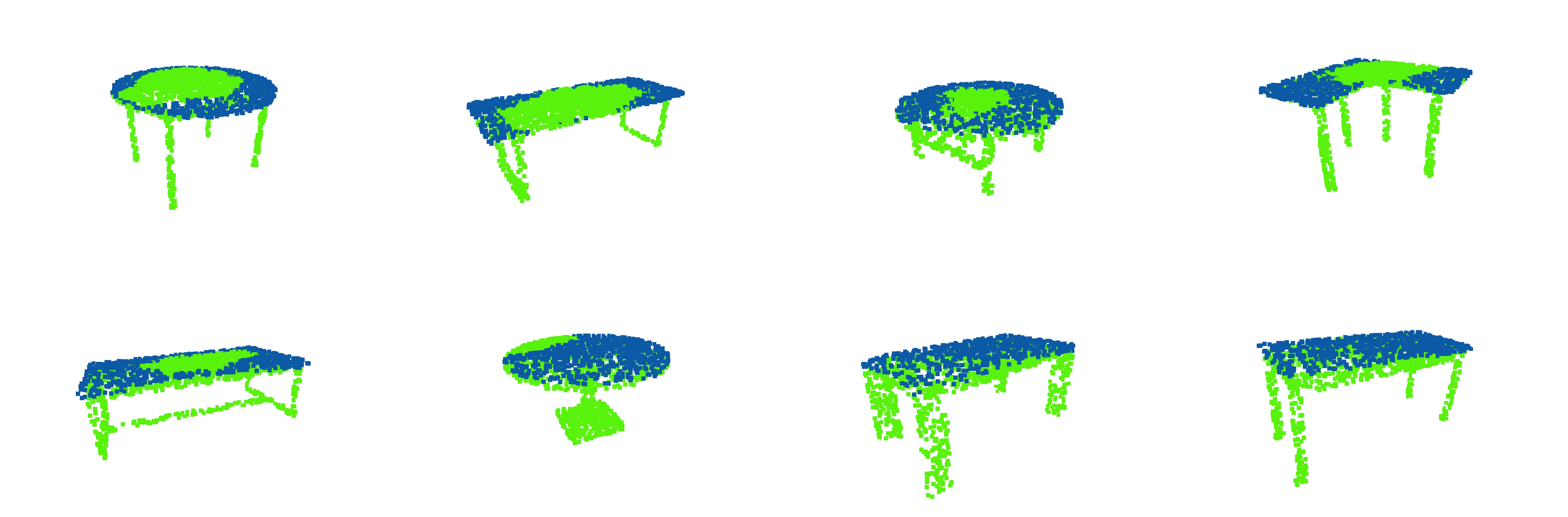
The result shows a fairly good performance of neural networks doing plane detection for objects from a single category. The accuracy could even possibly rise if a larger training set is prepared. The model seems to favor a table object with a more normal shape, i.e., a table with a square tabletop and four straight legs. For tables without a regular shape, the classification accuracy is relatively lower, and the model tends to misclassify the points in the middle of the tabletop.

The asymmetric network shows a similar test result, which comes out with an accuracy of 85.7117% and an IoU of 75.0279%. The plane detection results of the asymmetric network are shown in Figure 7 below.

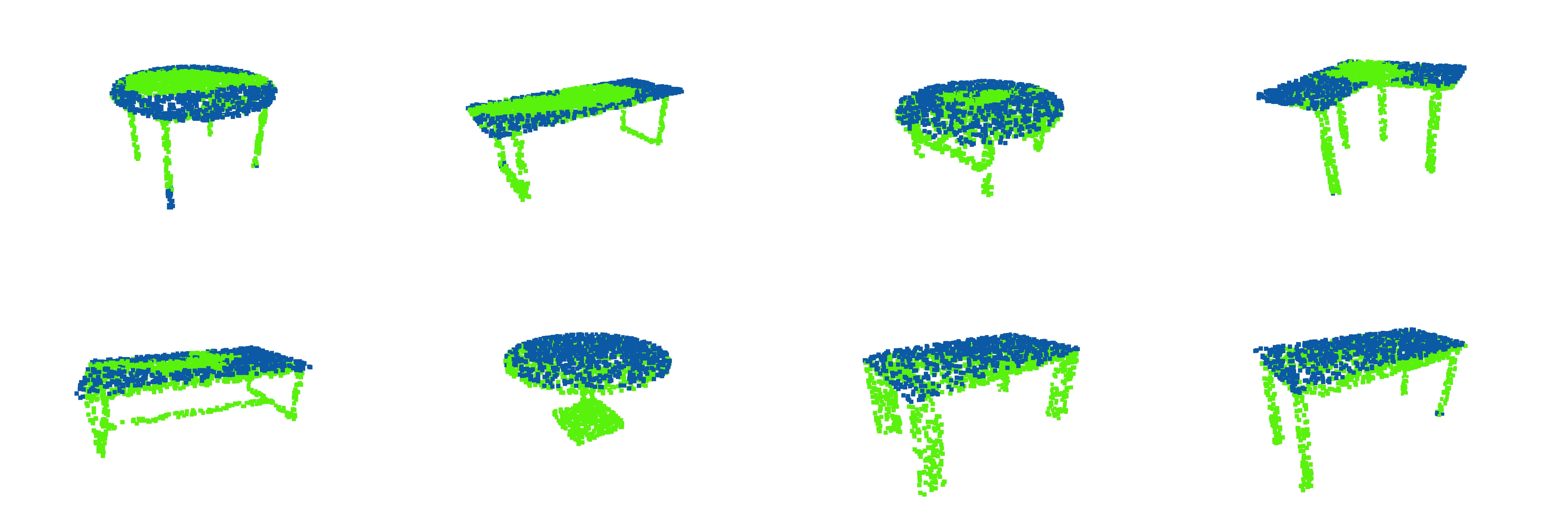
Similar to the results of the symmetric network, the model based on the asymmetric network shows a good performance on objects with a more regular shape. It may also fail to classify the points in the middle of the tabletop. Furthermore, the asymmetric network could also misclassify a few points on the legs of a table, which is shown in the 1st, 2nd, and 8th objects, and such a pattern is not observed in the results of the symmetric network.

Conclusion

In this experiment, although the asymmetric network shows a slightly higher classification accuracy, we cannot conclude that the asymmetric network has a better performance for doing the plane detection work. Since only one category of object is included in the experiment, the global vector generated in the symmetric function actually does not make an effort. In further experiments, we can introduce more categories of objects and see how the networks will work on more complicated shapes.

This experiment shows the potential of neural networks for doing plane detection. According to the experiment results, misclassification is resulting in holes on the detected planes. This is a not a very severe problem for plane detection tasks, as we can apply a 3D Hough transform afterwards, which is robust to missing and contaminated data, to the points of detected planar parts to generate the plane information.

All the code and data of this experiment can be found over my GitHub repository IsaacGuan/PointNet-Plane-Detection.