Mesh smoothing, also known as mesh denoising, is an important and widely discussed topic in geometry processing. Basically, a mesh smoothing method takes three steps: loading a mesh from a file; smoothing that mesh; outputting the mesh to a file. Recently, I implemented a few basic algorithms regarding mesh smoothing.
Selection of Mesh Library
There are a lot of mesh libraries that give us a data structure such that we can use to build a mesh for a 3D object. What I am using is the geometry-processing-js library. It is a library written in JavaScript which constructs a mesh based on half-edge. It also gives plenty of predefined functions regarding the components of a mesh e.g. half-edge, vertex, edge, face, etc. Besides, it also includes a linear algebra library which makes it handy for users to do matrix-vector operations.
Mesh Smoothing Algorithms
I implemented two algorithms for mesh smoothing, a mean filtering algorithm, and a weighted mean filtering algorithm.
Mean Filtering Algorithm
A most naïve mean filtering algorithm goes as follows:
Begin
Step 1: Create a hash map $\mathrm{positions}$ mapping each vertex with its position to be updated;
Step 2: For each vertex $\mathbf{v}$ in the mesh, calculate $\mathrm{positions}[\mathbf{v}]$ by the average position of the neighbor vertices in the one-ring neighborhood of $\mathbf{v}$;
Step 3: After the whole iteration, update the positions of vertices in the mesh by the hash map $\mathrm{positions}$.
End
However, if the object has some holes in it, this algorithm could cause the holes to enlarge after times of iteration, which is shown in Figure 1.
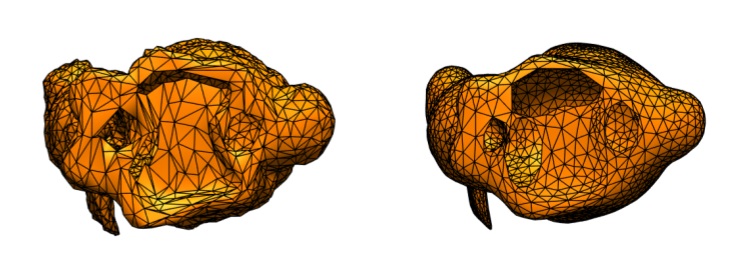
Sometimes, we don’t like such distortion, so it is necessary to preserve the boundary of holes on the mesh. We can add a step to the algorithm to constrain the vertices of boundary edges:
Begin
Step 1: Create a hash map $\mathrm{positions}$ mapping each vertex with its position to be updated;
Step 2: For each vertex $\mathbf{v}$ in the mesh, calculate $\mathrm{positions}[\mathbf{v}]$ by the average position of the neighbor vertices in the one-ring neighborhood of $\mathbf{v}$;
Step 3: To preserve the boundary of holes on the mesh, if vertex $\mathbf{v}$ is on the boundary, update $\mathrm{positions}[\mathbf{v}]$ to the original position of vertex $\mathbf{v}$ in the mesh;
Step 4: After the whole iteration, update the positions of vertices in the mesh by the hash map $\mathrm{positions}$.
End
Weighted Mean Filtering Algorithm
The weighting method simply weights each neighboring vertex by the area of the two faces incident to it. The weighted mean filtering algorithm goes like this:
Begin
Step 1: Create a hash map $\mathrm{positions}$ that maps each vertex to its position to be updated;
Step 2: For each vertex $\mathbf{v}$ in the mesh, traverse its neighborhood vertices. And for each neighbor vertex $\mathbf{v}^\ast$ calculate the weight value $w^\ast$ on each neighborhood vertex by adding the area of the two incident faces together;
Step 3: After the traversal of neighborhood vertices, calculate the total weight $w$ on the vertex $\mathbf{v}$ by accumulating every $w^\ast$, and calculate $\mathrm{positions}[\mathbf{v}]=\frac{\sum_{}w^\ast\cdot\mathbf{v}^\ast}{w}$;
Step 4: To preserve the boundary of holes on the mesh, if vertex $\mathbf{v}$ is on the boundary, update $\mathrm{positions}[\mathbf{v}]$ to the original position of vertex $\mathbf{v}$ in the mesh;
Step 5: After the whole iteration, update the positions of vertices in the mesh by the hash map $\mathrm{positions}$.
End
However, in the implementation, I found this could cause the faces of the mesh overlapping one another after several times of iterations, as the position of vertex could fall outside its one-ring neighborhood. As shown in Figure 2, overlapping occurs after 5 times of iteration.

In order to prevent such thing from happening, I tried to find those vertices which could fall outside its neighborhood during an iteration. The one-ring neighborhood of one vertex is actually a star-shaped polygon so that we can use the left-turn/right-turn check to decide whether the vertex is inside it or not.
To find out the star-shaped neighborhood of a certain vertex $\mathbf{v}$, we should first project all the neighbors onto the plane which is defined by vertex $\mathbf{v}$ and its normal vector $\mathbf{n}$. We can find the projection $\mathbf{q}=(x^\prime,y^\prime,z^\prime)$ of vertex $\mathbf{p}=(x,y,z)$ on the plane that defined by the normal $\mathbf{n}=(a,b,c)$ and vertex $\mathbf{v}=(x_0,y_0,z_0)$ in the way below.
There are following implicit geometric relationships between $\mathbf{p}$, $\mathbf{q}$, $\mathbf{n}$, and $\mathbf{v}$: $(\mathbf{q}-\mathbf{p})\parallel\mathbf{n}$ and $(\mathbf{q}-\mathbf{v})\perp\mathbf{n}$.
The following equation can be derived from $(\mathbf{q}-\mathbf{p})\parallel\mathbf{n}$:$$\begin{equation}\frac{x^\prime-x}{a}=\frac{y^\prime-y}{b}=\frac{z^\prime-z}{c}=t.\tag{1}\label{eq:1}\end{equation}$$
And from $(\mathbf{q}-\mathbf{v})\perp\mathbf{n}$, we can derive:$$\begin{equation}a(x^\prime-x_0)+b(y^\prime-y_0)+c(z^\prime-z_0)=0.\tag{2}\label{eq:2}\end{equation}$$
Combining $\eqref{eq:1}$ and $\eqref{eq:2}$, we can solve for $t$:$$\begin{equation}t=\frac{ax_0+by_0+cz_0-(ax+by+cz)}{a^2+b^2+c^2}.\tag{3}\label{eq:3}\end{equation}$$
Then we can solve for the projection $\mathbf{q}=(x^\prime,y^\prime,z^\prime)$ by combining $\eqref{eq:1}$ and $\eqref{eq:3}$.
As the data structure of mesh is based on half-edge, and all the faces are defined by half-edges in counterclockwise order. Thus, for each vertex $\mathbf{v}$, we can simply get the boundary edges of a star-shaped neighborhood in counterclockwise order, project them along with the position to be updated $\mathrm{positions}[\mathbf{v}]$ onto the plane that is defined by vertex $\mathbf{v}$ and its normal vector $\mathbf{n}$. Then we can do the left-turn/right-turn check on that plane to see whether the new position for vertex $\mathbf{v}$ $\mathrm{positions}[\mathbf{v}]$ is outside its neighborhood polygon or not.
So the modified algorithm goes as follows:
Begin
Step 1: Create a hash map $\mathrm{positions}$ that maps each vertex to its position to be updated;
Step 2: For each vertex $\mathbf{v}$ in the mesh, traverse its neighborhood vertices. And for each neighbor vertex $\mathbf{v}^\ast$ calculate the weight value $w^\ast$ on each neighborhood vertex by adding the area of the two incident faces together;
Step 3: After the traversal of neighborhood vertices, calculate the total weight $w$ on the vertex $\mathbf{v}$ by accumulating every $w^\ast$, and calculate $\mathrm{positions}[\mathbf{v}]=\frac{\sum_{}w^\ast\cdot\mathbf{v}^\ast}{w}$;
Step 4: Check whether $\mathrm{positions}[\mathbf{v}]$ falls outside its one-ring neighborhood. If so, use the mean filtering algorithm to update the new position;
Step 5: To preserve the boundary of holes on the mesh, if vertex $\mathbf{v}$ is on the boundary, update $\mathrm{positions}[\mathbf{v}]$ to the original position of vertex $\mathbf{v}$ in the mesh;
Step 6: After the whole iteration, update the positions of vertices in the mesh by the hash map $\mathrm{positions}$.
End
Results and Conclusion
As for the mean filtering algorithm, Figure 3 shows the results after applying it to different objects with different step numbers.

As for the weighted mean filtering algorithm, Figure 4 shows the results after applying it to different objects with different step numbers.

We can conclude that the results of both algorithms basically look alike, and both of them could cause the volume of the object to shrink if we apply too many times.
I have also uploaded the project to this blog: /projects/mesh-smoothing, we can go there to see how exactly the algorithms work.