Isaac's Blog

Implementation of Voronoi Diagram and Delaunay Triangulation

computational-geometry voronoi-diagram delaunay-triangulation
2017/12/22

The Voronoi diagram and the Delaunay triangulation are dual representations of a set of points to each other. Due to their wide applications in science and technology, the Voronoi diagram and the Delaunay triangulation play important roles in the field of computational geometry. In this post, I am going to introduce an implementation of an algorithm to derive both the Voronoi diagram and the Delaunay triangulation of a set of points in the plane.

Voronoi Diagram and Delaunay Triangulation

The Voronoi diagram of a set of points, also known as Thiessen polygons, is a partitioning of a plane into regions by a set of continuous polygons consisting of perpendicular bisectors of the connecting lines of two adjacent points. These regions are called Voronoi cells. And for each point in the set, there is a corresponding Voronoi cell consists of all points closer to that point than to any other.

The Delaunay triangulation of a set of points is dual to its Voronoi diagram. It is a collection of connected but non-overlapping triangles, and the outer circumcircle of these triangles does not contain any other points in this set.

Design of the Algorithm

There are a lot of ways to generate a Voronoi diagram from a set of points in the plane. In this implementation, I obtained the Voronoi diagram from generating its dual, the Delaunay triangulation. Generally speaking, for the set of $n$ points $P=\{\mathbf{p}_1,\mathbf{p}_2,\ldots,\mathbf{p}_n\}$ in $\mathbb{R}^2$, the algorithm goes in this way: the Delaunay triangulation of the set of points is firstly generated, then we calculate the center of the circumcircle of each triangle, and finally, we connect these centers with straight lines and form the polygon mesh generated from the vertices of the triangles.

Design of the Data Structure

I implemented this algorithm in the object-oriented language, so the design of the data structure is in the form of classes.

Point:

1
2
3
4
5
6
7
8
9
10
11
12
13
class Point
{
    public double x, y, z;
    public List<int> adjoinTriangles;
    public Point(double x, double y, double z)
    {
        this.x = x;
        this.y = y;
        this.z = z;
        adjoinTriangles = new List<int>();
    }
}

Voronoi edge:

1
2
3
4
5
6
7
8
9
10
class VoronoiEdge
{
    public Point start, end;
    public VoronoiEdge(Point start, Point end)
    {
        this.start = start;
        this.end = end;
    }
}

Delaunay edge:

1
2
3
4
5
6
7
8
9
10
class DelaunayEdge
{
    public int start, end;
    public DelaunayEdge(int start, int end)
    {
        this.start = start;
        this.end = end;
    }
}

Triangle:

1
2
3
4
5
6
7
8
9
10
11
12
13
class Triangle
{
    public int vertex1, vertex2, vertex3;
    public Point center;
    public double radius;
    public Triangle(int vertex1, int vertex2, int vertex3)
    {
        this.vertex1 = vertex1;
        this.vertex2 = vertex2;
        this.vertex3 = vertex3;
    }
}

On top of that, I defined a point list and a triangle list under the Collections class to store all the points in the point set $P$ and all the triangles during the procedure of triangulation as global variables:

1
2
3
4
5
class Collections
{
    public static List<Point> allPoints;
    public static List<Triangle> allTriangles;
}

Thus, in the Point class, DelaunayEdge class, and Triangle class, I can use an integer to represent the index of a certain point or triangle from the global lists and retrieve it directly.

Build up the Vonoroi Diagram

The algorithm of building up a Vonoroi diagram goes in this way:

Begin

Step 1: Obtain the Delaunay triangulation by generating the list of Delaunay edges.

Step 2: Traverse all the Delaunay edges.

Step 3: For each Delaunay edge, traverse the two triangle lists stored with the starting point and the endpoint, and find the two same triangles in the two lists which are the adjacent triangles of this Delaunay edge.

Step 4: Construct a Voronoi edge by connecting the two centers of the circumcircles of the two adjacent triangles and add it to the Voronoi edge list.

End

Conduct the Delaunay Triangulation

I planned to apply the Bowyer–Watson algorithm for computing the Delaunay triangulation. A most naïve Bowyer–Watson algorithm goes like this:

Begin

Step 1: Construct a “super” triangle that covers all the points from the point set, add it to the Delaunay triangle list.

Step 2: Insert points from the point set $P=\{\mathbf{p}_1,\mathbf{p}_2,\ldots,\mathbf{p}_n\}$ to the “super” triangle one by one.

Step 3: For each point $\mathbf{p}_i$ inserted, traverse the Delaunay triangle list to find all the triangles whose circumcircles cover this point $\mathbf{p}_i$ as invalid triangles, delete these triangles from the Delaunay triangle list and delete all the common edges of these triangles, and leave a star-shaped polygonal hole.

Step 4: Connect the point $\mathbf{p}_i$ to all the vertices of this star-shaped polygon, and add the newly formed triangles to the Delaunay triangle list.

Step 5: After all the points are inserted, obtain the Delaunay edge list from the Delaunay triangle list, and delete the edges from the Delaunay edge list that contains a vertex of the original “super” triangle.

End

The following pictures can better illustrate the key steps of this algorithm. As shown in Figure 1, when a new point is inserted, all the triangles whose circumcircles contain this point will be found. The common edges of these triangles, which are highlighted in yellow, will be deleted, leaving the star-shaped boundary in red.

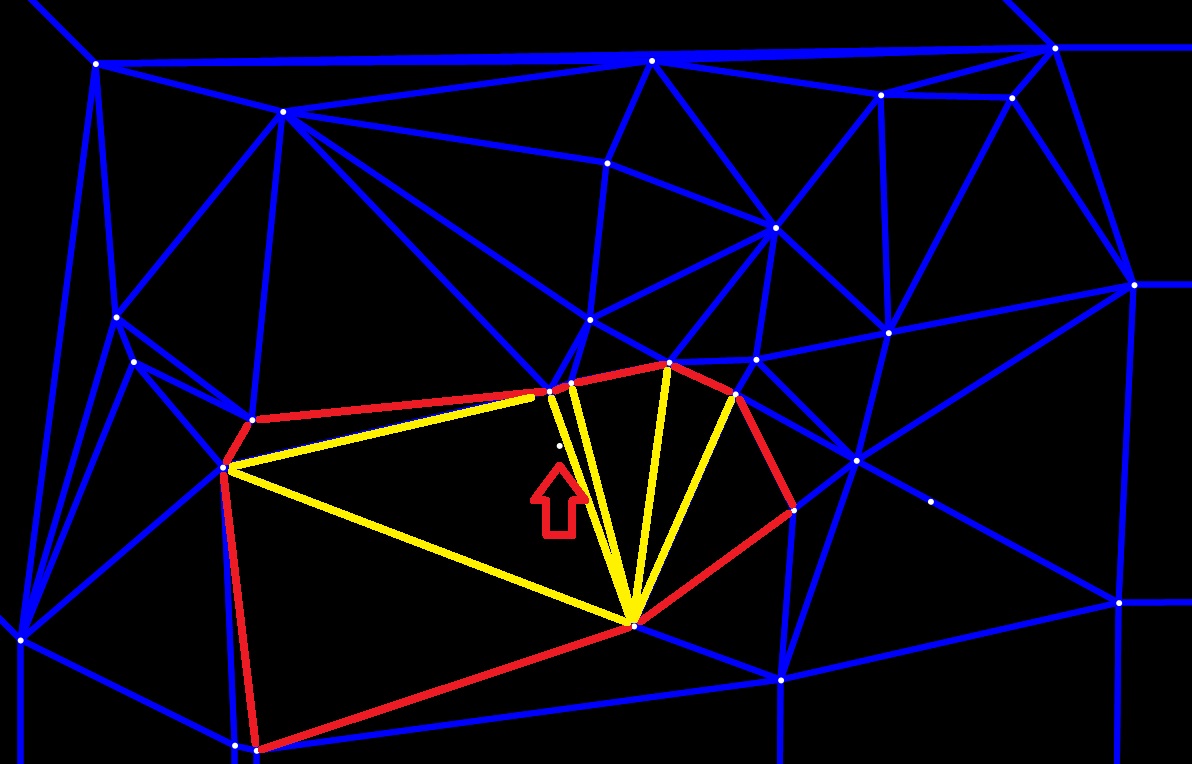
implementation of voronoi diagram and delaunay triangulation figure 1

Figure 1: A new point inserted.

And then, the inserted point will be connected to all the vertices of the star-shaped polygon, as shown in Figure 2, the new Delaunay triangles will be formed.

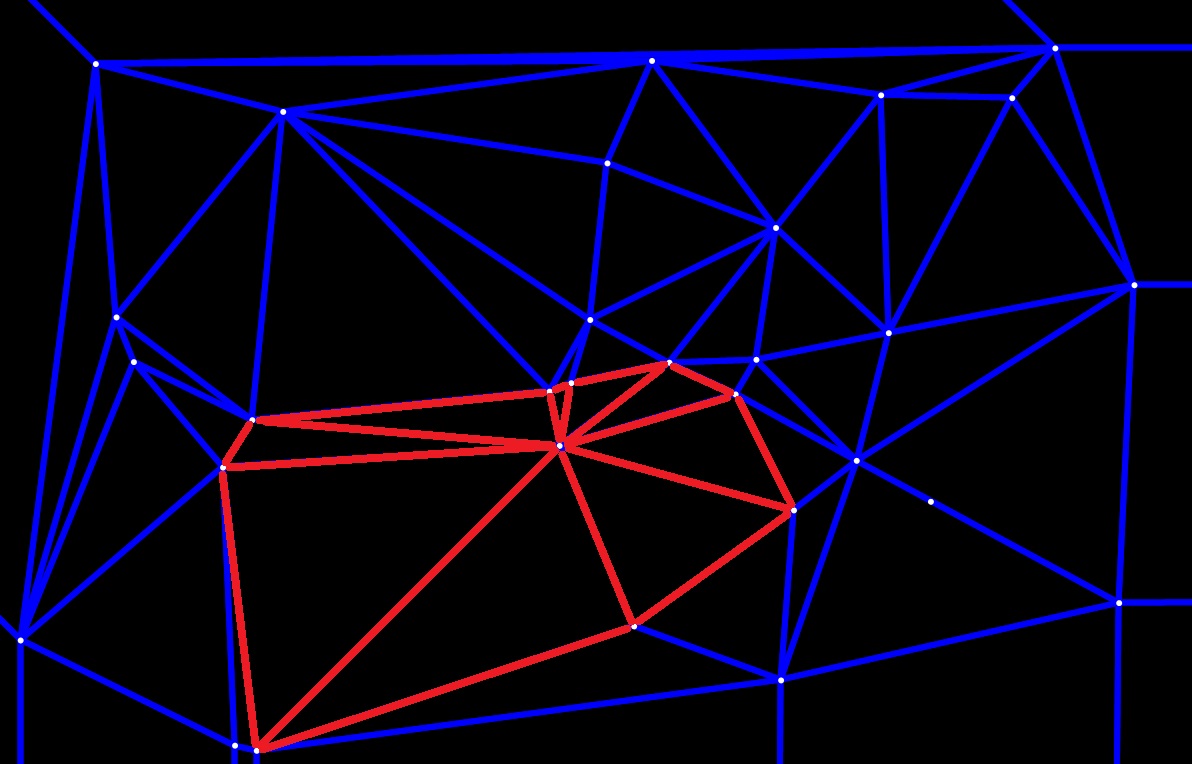
implementation of voronoi diagram and delaunay triangulation figure 2

Figure 2: Connecting to the inserted point.

However, the aforementioned naïve manner of Delaunay triangulation is clearly an $O(n^2)$ time algorithm that is incapable of handling a massive amount of points.

For improving its efficiency, we can first sort the set of points by x-coordinates and then use an open list and a closed list to store all the Delaunay triangles. In each time a point is inserted, all the triangles with circumcircles to the left of the inserting point are put into the closed list and removed from the open list. All the new triangles generated in an insertion are put into the open list. So in each time of insertion, we just have to traverse the open list to find the invalid triangles, the length of the sequential search of triangles is much reduced.

Besides, in order to derive the Voronoi diagram, when a new point is inserted, all the newly formed triangles that are incident on the point are put into the triangle list that is stored with the point.

Thus, the optimized algorithm goes as follows:

Begin

Step 1: Sort the points in the point set $P=\{\mathbf{p}_1,\mathbf{p}_2,\ldots,\mathbf{p}_n\}$ by x-coordinate.

Step 2: Construct a “super” triangle that covers all the points from the point set, add it to the open list.

Step 3: Insert points from $P$ to the “super” triangle one by one in ascending order of x-coordinates.

Step 4: For each point $\mathbf{p}_i$ inserted, traverse the open list to: 1) find all the triangles with circumcircles lying to the left of the point $\mathbf{p}_i$, delete these triangles from the open list and add them to the closed list; 2) find all the triangles with circumcircles covering this point $\mathbf{p}_i$ as invalid triangles, delete these triangles from the open list and the triangle list stored with $\mathbf{p}_i$, delete all the common edges of these triangles, leaving a star-shaped polygonal hole.

Step 5: Connect the point $\mathbf{p}_i$ to all the vertices of this star-shaped polygon, and add the newly formed triangles to the open list and the triangle list stored with $\mathbf{p}_i$.

Step 6: After all the points are inserted, merge the open list and the closed list into the Delaunay triangle list, obtain the Delaunay edge list from the Delaunay triangle list, and delete the edges from the Delaunay edge list that contains a vertex of the original “super” triangle.

End

Time Complexity of the Algorithm

The optimized algorithm for Delaunay triangulation takes $O(n\log n)$ time. As Delaunay triangulation is a planar graph, the number of triangles incident on one point is constant, so the procedure of finding adjacent triangles takes constant time and the time of generating the Voronoi diagram is $O(n)$. Therefore, the total running time of this algorithm is $O(n\log n)$.

Implementation of the Algorithm

This algorithm is implemented in C#. Figure 3 shows the result of the implementation of this algorithm, it is capable of handling massive input of 10000 points.

implementation of voronoi diagram and delaunay triangulation figure 3

Figure 3: Voronoi diagram and Delaunay triangulation for 10000 points.

The GitHub repository of this implementation is IsaacGuan/Voronoi-Delaunay.

CATALOG
  1. 1. Voronoi Diagram and Delaunay Triangulation
  2. 2. Design of the Algorithm
    1. 2.1. Design of the Data Structure
    2. 2.2. Build up the Vonoroi Diagram
    3. 2.3. Conduct the Delaunay Triangulation
  3. 3. Time Complexity of the Algorithm
  4. 4. Implementation of the Algorithm
Archive Tag
Total : 12
2020
2019
2018
2017
geometry-processing shape-context instance-segmentation data-preprocessing class-imbalance biking trip hello-world hough-transform parameterization plane-detection computational-geometry voronoi-diagram delaunay-triangulation mesh-smoothing deep-learning pointnet ubuntu rapter tutte-embedding convex-hull